Technical Articles and Product Descriptions

Reference Materials

Additional Products

Race Engine Technology Magazine

This section crams a lot of information into a short space, so a little extra time spent reading it can pay dividends later on. (To engineering readers, please forgive the liberties taken in the interest of brevity.)

Components in a vibrating system have three properties of interest. They are: mass (weight), elasticity (springiness) and damping (dissipation). Most physical objects have all three properties, but in many cases one or two of those properties are relatively insignificant and can be ignored (for example, the damping of a block of steel, or in some cases, the mass of a spring).

The property of MASS (weight) causes an object to resist acceleration. It also enables an object to store energy, in the form of velocity (kinetic) or height (potential). You must expend energy to accelerate a mass or to lift a mass. If you decelerate a moving mass, or drop a lifted mass, the energy it took to accelerate it or to lift it (as applicable) can be recovered.

The property of ELASTICITY enables an object to store energy in the form of deflection. A common example is a spring, but any piece of metal has the property of elasticity. That is, if you apply two equal and opposite forces to opposite sides of it, it will deflect. Sometimes that deflection can be seen; sometimes it is so small that it can't be measured with a micrometer. The size of the deflection depends on the size of the applied force and the dimensions and properties of the piece of metal. The amount of deflection caused by a specific force determines the "spring rate" of the metal piece. Note that all metals (in the solid state) have some amount of elasticity.

You must expend energy to deflect a spring. The spring stores most of the energy required to deflect it. When you release a deflected spring, the stored energy can be recovered.

The term DAMPING is frequently misunderstood. The property of damping enables an object to DISSIPATE energy, usually by conversion of kinetic (motion) energy into heat energy. The misnamed automotive device known as a "shock absorber" is a common example of a damper. If you push on the ends of a fully extended "shock absorber" (so as to collapse it) the rod moves into the body at a velocity related to how hard you are pushing. Double the force and the velocity doubles. When the "shock" is fully collapsed, and you release your hand pressure, nothing happens (except maybe you drop it). The rod does not spring back out. The energy (defined as a force applied over a distance) which you expended to collapse the damper has been converted into heat which is dissipated through the walls of the shock absorber.

The resonant frequency of an object (or system) is the frequency at which the system will vibrate if it is excited by a single pulse. As an example, consider a diving board. When a diver bounces on the end of the board and commences a dive, the board will continue to vibrate up and down after the diver has left it. The frequency at which the board vibrates is it’s resonant frequency, also known as it’s natural frequency. Another example is a tuning fork. When struck, a tuning fork "rings" at it’s resonant frequency. The legs of the fork have been carefully manufactured so as to locate their resonant frequency at exactly the acoustic frequency at which the fork should ring.

The resonant frequency of a system (symbolized "ω _n", pronounced "omega-sub-n") is determined by both the mass properties and the elasticity properties of the system.

If you increase the mass property or decrease the elasticity property of a system, the resonant frequency will decrease according to the relationship:

ω_n = √(k/m)

where "k" is the appropriate elasticity value (spring rate) and "m" is the appropriate mass value.

Note that damping has no effect on the system resonant frequency. Damping simply dissipates energy from a vibrating system, and thereby limits the amount of energy which can feed back into the system, and so limits the amount of "out-of-control" vibration which can occur near resonance.

A waveform is a pictorial representation of a vibration. For illustration purposes, Figure 1 shows waveform representing the instantaneous torque of a typical 8-cylinder engine.

The term frequency occurs often in the discussion of vibration. The frequency of a waveform (torque variation, in this case) is the number of times per second that the waveform repeats itself, while the order of a waveform is the number of times that the waveform repeats itself during a particular event (such as one revolution of a crankshaft).

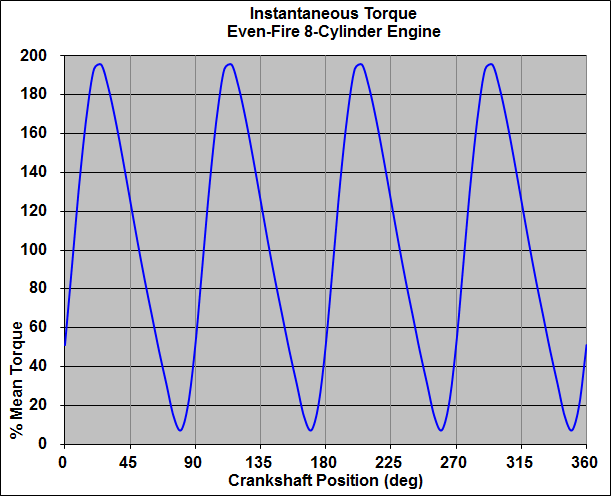
FIGURE 1
Waveform Example

The waveform shown in Figure 1 is a 4^th order torsional vibration (four spikes per rotation). The frequency of the vibration changes with ngine RPM. For example, at 4600 RPM the frequency of the 4^th order vibration is 307 cycles per second, or "Hertz" (HZ), the units of cycles per second.

(The frequency value 307 is calculated as follows: 4600 revolutions-per-minute divided by 60 seconds-per-minute = 76.7 revolutions-per-second, multiplied by 4 pulses-per-revolution = 307 HZ. Using the same arithmetic, the excitation frequency of a 4^th-order vibration at 800 RPM is 53 HZ.)

NOTE: Torsional Excitation by Piston Engines is covered in Engine Technology.